Transport properties of magnetic ultra-fine particles play a significant role in the problem of long-term stability of magnetic fluids. Usually, in colloidal stability research mainly the agglomeration problems as well as the magnetophoretic transfer of ferroparticles under the effect of a nonuniform magnetic field are taken into account. If high temperature gradients are present, the long-term stability of ferrocolloids is effected also by a thermophoretic transfer of particles.

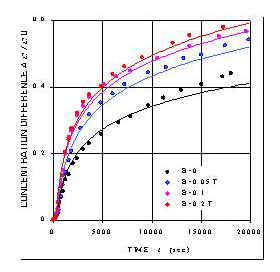
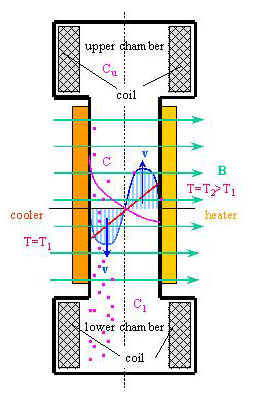
The Soret effect measurements are performed employing a thermal diffusion column consisting of a long vertical flat channel and two separations chambers (see Fig. 1). Both the particle transfer across the channel by thermodiffusion and the thermal convection of fluid in vertical direction cause a development of concentration difference in separation chambers D C=C_l-C_u. We determine the particle concentration C_u and C_l measuring the resonance frequency of a LC

oscillators the inductance coils of which are mounted inside both separation chambers. From unsteady separation curves D C= f(t) (see Fig. 2) we calculate the Soret coefficient of particles employing a column theory which is modified taking into account both the thermal as well as the concentration-driven convection in the channel. Experiments indicate a strong dependence of thermophoretic mobility of ferrite particles on magnetic flux density B as well as confirm the theoretically predicted anisotropy of magnetic Soret effect [2].

References

1. E. Blums. Some New Problems of Complex Thermomagnetic and Diffusion Driven Convection in Magnetic Colloids, J. Magn. and Magn. Materials, 1995, 149, Nos. 1-2, 111-115.

2. E. Blums, S. Odenbach, A. Mezulis, M. Maiorov. Soret Coefficient of Nanoparticles in Ferrofluids in the Presence of a Magnetic Field, Physics of Fluids, 1998, 10, No. 9, p. 2155-2163.